分散分析(ANOVA:analysis of variance)は、イギリスの統計学者フィッシャー(R.A.Fisher)によって開発されました。
帰無仮説&対立仮説
分散分析では、母平均の差を検定します。

母平均の差の検定といえば、t検定がありましたね。2群の母平均の差はt検定、3群以上なら分散分析を用いると覚えておいてください。2群で分散分析を用いると、結果的にt検定していることになります。
平均値を扱うので、従属変数は量的変数になり、独立変数は質的変数です。
帰無仮説と対立仮説は以下とおりです。
対立仮説:群の母平均の中に等しくないものがある
以下のように、A群、B群、C群という3つの群を想定するとき、それぞれの平均が等しいという帰無仮説(μA=μB=μC)が棄却されれば、群の中に異なる母平均があるということですが、どの群が異なる値なのかはわかりません。
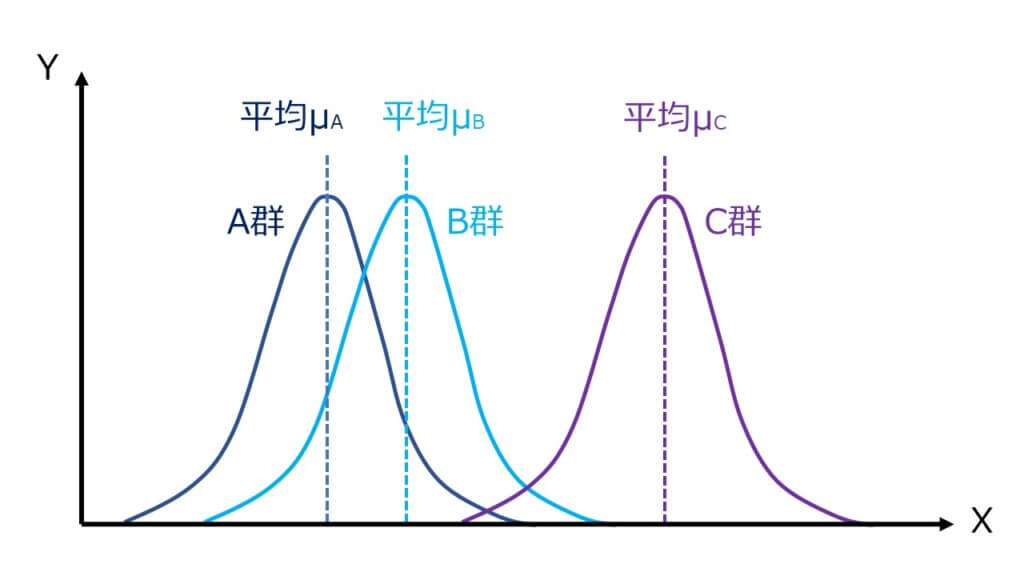

A群だけ異なる値かもしれないし、全部違う値かもしれません。
F値&P値
F値=(群の不偏分散)/(残差の不偏分散)
このF値は、「偶然による誤差(残差の不偏分散)」に比べて「群による誤差(群の不偏分散)」が十分大きいかどうかを調べる値です。
そしてこのF値が求まればF分布表からP値が求まるので、検定ができるというわけです。

P値とは「帰無仮説の下で実際にデータから計算された統計量よりも極端な統計量が観測される確率」でしたね。
F値の「F」は分散分析を開発したフィッシャーのFです。
このF値を求めるときに分散を使うので、分散分析と呼ばれています。
要因&水準
分散分析では比較を行う切り口を「要因」といいます。
切り口が1つであれば「1要因の分散分析」、2つであれば「2要因の分散分析」といいます。
例えば有名なホーソンの実験、照明の明るさによる作業効率への影響を調査したものですが、これは「照明の明るさ」という1要因の実験ということになります。
他に、男女別で実験したのなら「性別」という要因も加わり2要因となります。
さらに水準とは、要因に含まれる項目のことです。
この場合の水準は、以下のように4水準ですね。
| 被験者 | ||||
|---|---|---|---|---|
| 要因 | 性別 | 照明 | ||
| 水準 | 男性 | 女性 | 明るい | 暗い |
主効果&交互作用
分散分析では、要因が2つ以上ある場合に、主効果だけでなく要因同士の交互作用を検定できます。
主効果とは因子単独の効果のこと、交互作用とは複数の因子の組み合わせによる効果のことです。
例えば、先ほどの例では、性別と照明の明るさという2要因がありましたが、照明が明るい方が作業効率が良いという単純なものではなく、男性の場合は明るい方がよく、女性の場合は暗い方が良いというように要因同士が交互に作用すること、これが交互作用です。
被験者間&被験者内
被験者内計画は、同じ被験者が全ての水準を体験します。
先ほどの例では照明の明るい暗いを同一人物が経験するということです。
被験者間計画は、別々の人に対して各水準を割り当てます。
別々の人だと、個人差が入ってくるので実験としては好ましくありませんが、同一人物であっても前の実験の影響が後の実験に影響する「残留効果」がありますので、それも良くありません。
被験者内と被験者間を混ぜて行う場合、「混合」分散分析と呼びます。
対応の有無
対応の有無という概念を理解しましょう。
2つの群にランダムで被験者を割り当てれば「対応のない」、2つの群に同一の被験者またはマッチングによって各群の被験者を割り当てる場合は「対応のある」になります。

ということは、「被験者内」であれば、必ず「対応のある」になりますね。
まとめ
分散分析という名称ですが、分散同士を比較するのではなく、母平均同士を比較する点に注意です。
ホーソンの実験では、照明の作業速度への影響を測るため、常に明るい状況で作業するグループと、回数を追うごとに照明が暗くなるグループとに分けて実験をしました。
この場合の独立変数と従属変数は、
従属変数:「作業速度」
これは「1要因の対応のない被験者間の分散分析」ということになりますね。
過去問
第2回 問80
1要因分散分析の帰無仮説として、正しいものを1つ選べ。
① 全ての水準の母平均は等しい。
② 全ての水準間の母分散は等しい。
③ 全ての水準の母平均は等しくない。
④ 少なくとも1組の水準間の母平均は等しい。
⑤ 少なくとも1組の水準間の母平均は等しくない。
分散分析は、母平均に有意差があるかどうかを検定します。
ということで、選択肢①が正解です。
帰無仮説ですから「等しい」ことを仮定します。
第4回 問82
観察者の有無が作業に及ぼす影響を見る実験において、参加者を、作業時に観察者がいる群といない群に分け、各郡の参加者に、単純課題条件と複雑課題条件の双方を課した。
この結果の分析方法として最も適切なものを1つ選べ
① 2要因混合分散分析
② 2要因被験者間分散分析
③ 2要因被験者内分散分析
④ 複数個の1要因被験者間分散分析
⑤ 複数個の対応のある平均値のt検定
事例より、要因としては観察者の有無と課題条件という2要因、観察者の有無については2群に分けるので「被験者間」、そして課題条件は同一人物が2条件を経験するので「被験者内」になるため、混合分散分析です。
2要因(2水準×2水準)ですからt検定を用いることはありません。
ということで選択肢①が正解です。
第2回 問136
網膜像差が奥行き知覚手掛かりとして有効であるかを検討する目的で実験を行った。
網膜像差が0分、6分、12分、18分の4種類からなるランダムドットステレオグラムを各実験参加者にランダムな順序で呈示した。
実験参加者はランダムドットステレオグラムを観察し、実験者から渡されたノギスを用いて見かけの奥行き量を再生した。
この実験データから網膜像差の4つの条件で再生された奥行き量の平均に差があるかを検討するための統計的方法として、最も適切なものを1つ選べ。
① 対応のある1要因分散分析
② 対応のある4要因分散分析
③ 対応のない1要因分散分析
④ 対応のない4要因分散分析
⑤ 対応のある2標本の平均の差の検定
まず、平均の差が有意であるかどうかの検定なので分散分析かt検定です。
事例では被験者それぞれに対して各水準(0分、6分、12分、18分)を実験する「被験者内」なので「対応のある」分散分析になります。
要因としては、ランダムドットステレオグラムという1要因(4水準)です。
ということで選択肢①が正解です。
選択肢⑤のような2標本ではありません。
第3回 問59
石けんの香りが机を清潔に保とうとする行動に影響を与えるかについて実験を行った。
香りあり条件と香りなし条件を設けて、机の上の消しくずを掃除する程度を指標として検討した。
その結果、全体的には香りあり条件と香りなし条件の差が検出されなかったが、尺度で測定された「きれい好き」得点が高い群は、全体として「きれい好き」得点が低い群よりもよく掃除をした。
さらに、高い群では香りあり条件と香りなし条件の差は明瞭でなかったが、低い群では、香りあり条件が香りなし条件よりも掃除をする傾向が顕著に観察された。
この実験の結果の理解として、正しいものを1つ選べ。
① 交互作用はみられなかった。
② 実験要因の主効果は有意であった。
③ 「きれい好き」要因の主効果は有意ではなかった。
④ 実験要因の主効果と交互作用が有意であった可能性が高い。
⑤ 「きれい好き」要因の主効果と交互作用が有意であった可能性が高い。
この実験は「香りの有無」「綺麗好きの程度」の2要因についての実験で、独立変数と従属変数は以下の通りです。
独立変数:「香りの有無(2水準)」「綺麗好きの程度(2水準)」
従属変数:「机の上の消しくずを掃除する程度」
① 交互作用はみられなかった。
間違いです。「香りの有無」「綺麗好きの程度」の2要因が交互に作用しています。
② 実験要因の主効果は有意であった。
間違いです。全体的には香りあり条件と香りなし条件の差が検出されなかったわけですから主効果はありません。
③ 「きれい好き」要因の主効果は有意ではなかった。
間違いです。「きれい好き」要因の主効果は有意でした。従属変数に影響を与えてましたね。
④ 実験要因の主効果と交互作用が有意であった可能性が高い。
間違いです。全体的には香りあり条件と香りなし条件の差が検出されなかったわけですから主効果は有意ではありません。
⑤ 「きれい好き」要因の主効果と交互作用が有意であった可能性が高い。
これが正解です。
第5回 問59
学習方法の違いにより学習内容の習得度に差があるかを検討する研究を行った。まず、参加した80名の生徒を無作為に2群(各40名)に分割して事前テストを行い、両群の能力が同等であることを確認した。そこで、一方を講義形式で学習する群、他方を協同学習で学習する群とし、学習後に事後テストを行った。事後テストの平均値(標準偏差)は、講義形式群67.34(9.12)、協同学習群76.40(8.79)であった。また、事前テストと事後テストの得点間の相関係数は、講義形式群0.66、協同学習群0.54であった。学習方法の違いにより習得度に差があるかを検討する分析法として、最も適切なものを1つ選べ。
① 2群の事後テストの平均値を対応のあるt検定で分析する。
② 2群の事後テストの平均値を対応のないt検定で分析する。
③ 2群の事前テストと事後テストの相関係数を対応のあるt検定で分析する。
④ 2群の事前テストと事後テストの相関係数を対応のないt検定で分析する。
⑤ 2群の事後テストの平均値と相関係数を被験者間2要因分散分析で分析する。
選択肢②が正解です。
次の記事
次は、因子分析について。




コメント