独立変数と従属変数の関係性を調べるのが「実験」です。
これらの変数には量的変数(間隔尺度や比例尺度)と質的変数(名義尺度や順序尺度)があり、量的変数を扱う場合は「散布図」、質的変数を扱う場合は「クロス集計表」で分析します。
相関係数
量的変数同士の関係性を「相関」と呼びます。
質的変数同士の関係性を「連関」と呼びます。
積率相関係数
直線的な「相関」の程度を表す係数が「ピアソンの積率相関係数」です。
例えば実験室で、部屋の温度Xに対して被験者の発汗量Yを求めたときに、XとYが直線関係にあれば(温度1℃上がると発汗量が2倍になるとか)、ピアソンの積率相関係数が「1」に限りなく近い値になります。
Xが大きくなるとYも大きくなる場合「正の相関」、Xが大きくなるとYは小さくなる場合「負の相関」があると言います。

発汗量Yは室温Xだけではなく、その他の環境や本人の心理的状況も影響するので、そのような独立変数以外の従属変数に影響する因子を「剰余変数」と呼ぶのでしたね。
下図のように、独立変数と従属変数の相関をみるには、横軸にX、縦軸にYをとった「散布図」を描けばわかります。
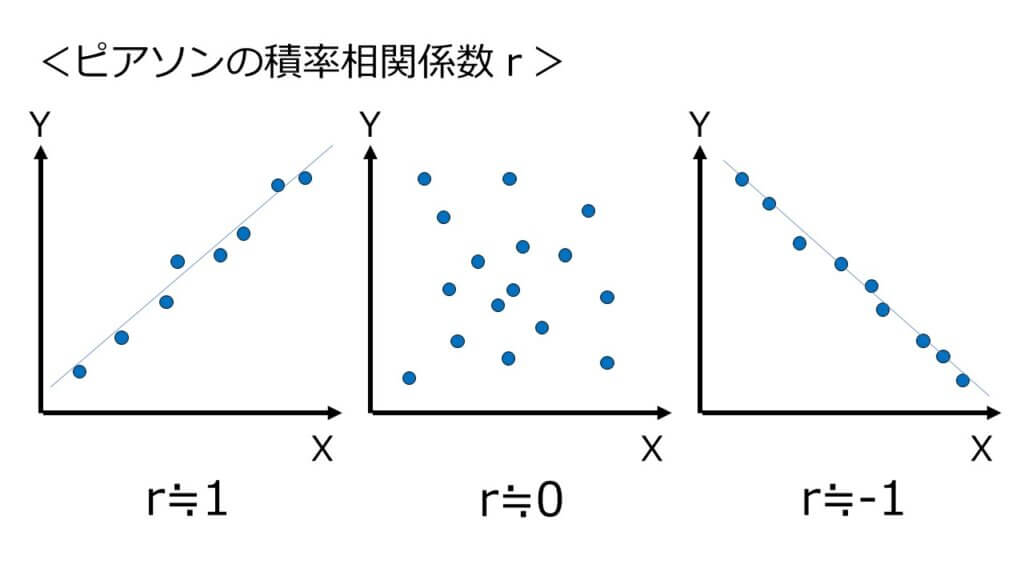
このように量的変数と量的変数の直線関係を表す指標が「ピアソンの積率相関係数」です。
相関係数の特徴は以下の通りです。
・単位は無い
・「−1」から「1」の値をとる
・「1」に近いときは正の相関
・「−1」 に近いときは負の相関
順位相関係数
ピアソンの積率相関係数は、直線的な相関の程度を評価しましたが、順位相関係数は直線的でない相関も含めて相関の程度を評価します。
ピアソンの積率相関係数は、母集団が正規分布などを想定できるパラメトリック、順位相関係数は母集団が想定できないノンパラメトリックな場合に用いられます。
順位相関係数には、「スピアマンの順位相関係数」や「ケンドールの順位相関係数」があります。
偏相関係数&部分相関係数
3つ以上の変数がある場合に、この中から取り出した2変数の相関係数を「偏相関係数」や「部分相関係数」と言います。
例えば、「かき氷の売れ行き」と「扇風機の売れ行き」の2つの相関を考えた時、これらには相関があるように見えます。
でもよく考えてみると、直接的な相関はなく、「気温」という媒介変数によって相関があるように見えているだけであることがわかります。
なので本来の「かき氷の売れ行き」と「扇風機の売れ行き」の相関を調べるためには、「気温」という第3の因子を除外して考えなければなりません。
ということで、第3の因子の影響を除いた相関係数である「偏相関係数」を用いて相関関係を評価すれば、「かき氷の売れ行き」と「扇風機の売れ行き」の相関はあまり強くないことがわかるでしょう。
このように、実際には相関関係がないのにあるように見える相関を「疑似相関」と呼びます。
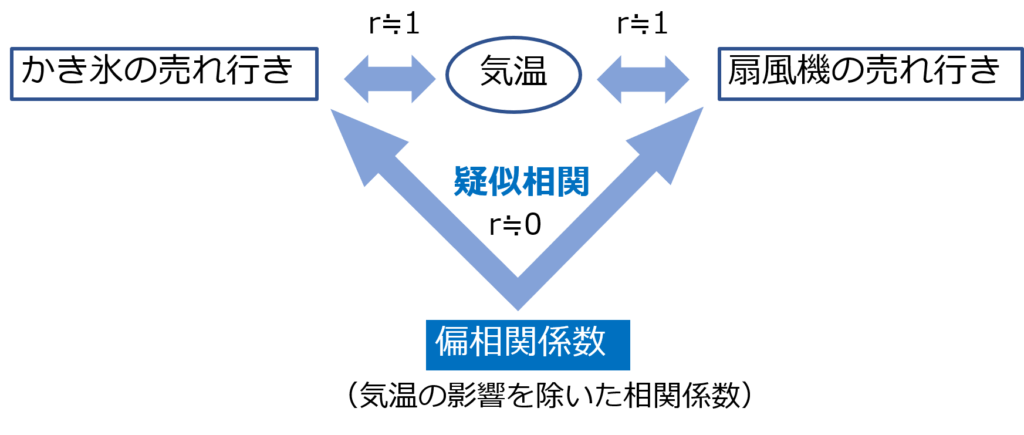
3つ以上の変数がある場合、ある変数が他の変数間の相関に影響を与えていることがあり、偏相関係数を算出することで調べたい変数同士の相関関係を見ることができます。
部分相関係数も偏相関係数と同じく、3つ以上の変数がある場合に、3変数のうちの2変数に関して第3の変数の影響を除外して考えた2変数間の相関係数ですが、偏相関係数は2変数両方について第3の変数の影響を除外するのに対して、部分相関係数は2変数のうち一方について第3の変数の影響を除外したものです。

部分相関係数は、重回帰分析における独立変数の選択に用いられます。
連関係数
これまで見てきたのは、量的変数(間隔尺度や比例尺度)から散布図を扱う例でした。
ここでは量的変数ではなく質的変数(名義尺度や順序尺度)からクロス集計表を扱う例を見ていきます。
四分点相関係数&クラメールの連関係数
例えば、体重や温度は量的変数ですが、性別や資格などは質的変数です。
このような質的変数を扱う場合は以下のようなクロス集計表が用いられます。
以下の表では、男性で公認心理師資格のある人は20,321人、などという意味です。
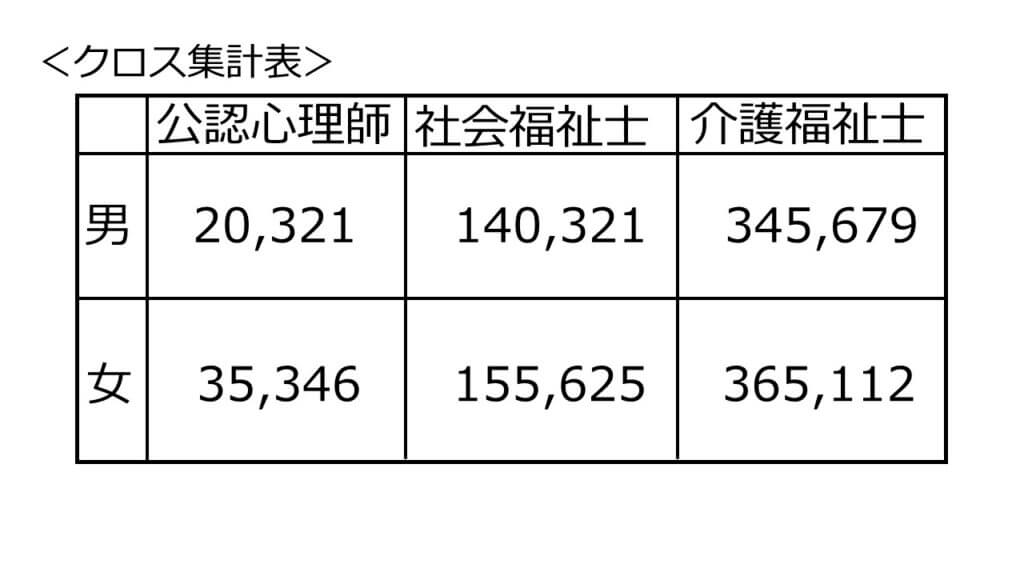
量的変数のときは「相関」と呼びましたが、質的変数を扱うときは「連関」と呼び、「連関係数」で見積もれます。

上のクロス集計表を見ると、女性の方が福祉系の国家資格の合格率が高そうだなーとか、連関を感じますね。
2×2のクロス集計表にのみ適用される連関係数としては、「四分点相関係数」、それ以上のクロス集計表には「クラメールの連関係数」が用いられます。
四分点相関係数は、2×2クロス集計表で変数が名義尺度の場合にしか使えません。
これら連関係数を算出するには、「カイ2乗検定」を行います。
まとめ
尺度によって関連性を評価する「係数」を以下のように使い分けます。
特に量的変数(間隔尺度、比例尺度)同士の相関を調べるときは、ピアソンの積率相関係数やスピアマンの順位相関係数が用いられますが、ピアソンの積率相関係数は直線的な相関、スピアマンの順位相関係数は直線以外も含めた相関を見積もれます。
| 名義尺度 | 順序尺度 | 間隔尺度 | 比例尺度 | |
|---|---|---|---|---|
| 名義尺度 | 四分点相関係数 クラメールの連関係数 |
順位相関比 | 相関比 | 相関比 |
| 順序尺度 | 順位相関係数 | 順位相関係数 | 順位相関係数 | |
| 間隔尺度 | 積率相関係数、順位相関係数 | 積率相関係数、順位相関係数 | ||
| 比例尺度 | 積率相関係数、順位相関係数 | 積率相関係数、順位相関係数 |
上の表にあるように、順位相関係数は順序尺度で用いられるだけでなく、間隔尺度や比例尺度のような量的変数でも用いられます。
名義尺度同士の相関を見る「連関係数」には、四分点相関係数とクラメールの連関係数があることも、しっかり押さえておいてください。
過去問
第3回 問82
① 偏相関係数
② 順位相関係数
③ 積率相関係数
④ 部分相関係数
⑤ 四分点相関係数
クロス集計表のような質的変数同士の関係性を示す指標としては、四分点相関係数やクラメールの連関係数があり、特に2×2のクロス集計表の場合は「四分点相関係数」が用いられます。
ということで選択肢⑤が正解です。
第1回(追試)問82
① F分布
② t分布
③ 2項分布
④ 正規分布
⑤ カイ2乗分布
クロス集計表の連関の検定では、四分点相関係数(ファイ係数)やクラメールの連関係数が用いられますが、この時に「カイ2乗値」を求めることが必要になるため、選択肢⑤「カイ2乗分布」が用いられます。
次の記事
次は、統計的仮説検定について。




コメント