母集団について仮定された仮説を検証するために「統計的仮説検定」が行われます。
例えば、平均値に差があるかどうか、分散に差があるかどうかなど。
以下のような流れで進められます。
②帰無仮説と対立仮説を立てる
③相関係数を計算する
④検定表で相関があるかどうかを検定する
散布図でデータを可視化するところは前回やりましたので、ここでは帰無仮説と対立仮説から見ていきましょう。
帰無仮説&対立仮説
母集団について仮定された仮説を、以下の例で考えてみます。
例えば、公認心理師国家試験の合格率が以下の表のとおりだったとします。
表を見ると、なんとなく女性の方が合格しやすいようにみえます。
恐らく男性の合格率と女性の合格率に有意差があることは間違いなさそうですが、偶然3回とも女性の方が高くなってしまった可能性もあります。
| 公認心理師国家試験 | 男性 | 女性 |
|---|---|---|
| 第1回 | 49% | 55% |
| 第2回 | 46% | 51% |
| 第3回 | 48% | 53% |
ということで、「女性の方が男性より公認心理師に合格しやすい」という仮説を立てます。
この仮説が正しいことを証明したいとき、まずは「有意差がない」という帰無仮説を立てます。
つまり、3回とも女性の合格率が高かったのは偶然だということですね。
この帰無仮説を否定することによって、「有意な差がある」と結論付けます。
帰無仮説とはその名の通り、無に帰すための仮説なので否定するために立てる仮説です。
帰無仮説の逆の仮説を対立仮説と呼びます。
この対立仮説が本来証明したい内容です。
これを帰無仮説を否定することによって証明します。
回りくどいのですが、差があることを証明するよりも、差がないことを否定することのほうがはるかに容易なのです。
ただしもし、帰無仮説が棄却されなかったとしても、帰無仮説が正しいということにはなりませんので注意です。
白黒つけられないという解釈が正しいです。
有意水準&P値
帰無仮説を否定するとき、当然ですが100%否定することはできません。
なぜなら実験結果は母集団全体ではなくあくまでも標本だからです。
先ほどの例では、女性の方が合格率は高そうだと思えても、100%そうだとは言い切れません。
そこでたいていの場合、95%以上の確率で帰無仮説が否定できれば、対立仮説を採択します。
それでも5%は誤ってしまうわけですが。
このときに設定した5%という水準を「有意水準」と呼んでいます。
つまり有意水準とは、「帰無仮説の下で実際にデータから計算された統計量よりも極端な統計量が観測される確率」がその水準を下回った時に「有意差あり」と結論づける基準です。
この「帰無仮説の下で実際にデータから計算された統計量よりも極端な統計量が観測される確率」を「P値」といいます。
繰り返しますが、帰無仮説は基本的には誤りである確率が高いので、棄却して帰無仮説を否定することを目指しますが、帰無仮説が正しい確率も小さいながらあるわけです。
先ほどの例では、明らかに女性の方が合格率が高そうだと思うのですが、偶然3回ともたまたまそうなってしまった可能性もあります。
このような帰無仮説が正しいにも関わらず、帰無仮説を棄却して誤ってしまう危険率のことを「有意水準」というわけです。
有意水準は0.05(5%)という値がよく用いられ、0.05をP値が下回れば、帰無仮説が棄却され対立仮説が採択されるので、目的達成というわけです。
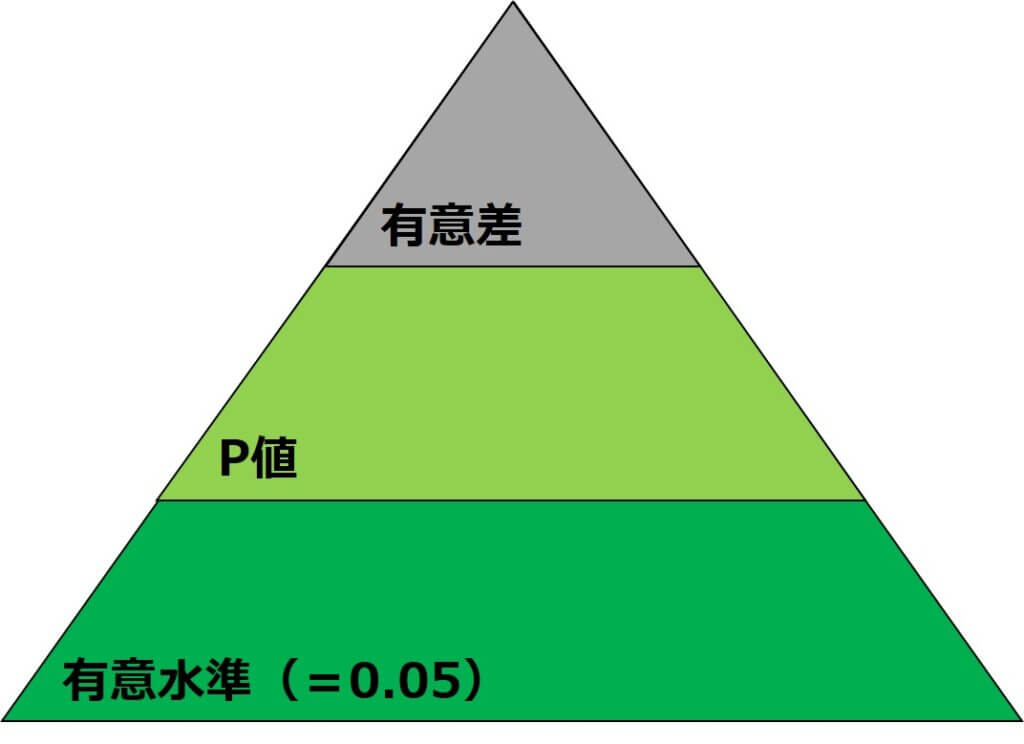

Pは「Probability=確率」という意味ですね。
相関係数
前回学んだ相関係数は、変数間の相関を示す値でしたが、相関係数の検定の帰無仮説と対立仮説は以下のようになります。
対立仮説:相関係数≠0
相関係数のP値が有意水準0.05を下回った場合「相関係数が0ではなさそう」ということは言えますが「相関が高い」ということは言えません。
P値は相関係数の大小だけでなくデータの数に依存するので、相関係数が高いことと検定が有意であることは、別モノです。
統計的仮説検定
それではどのように帰無仮説を棄却するのでしょう。
それが統計的仮説検定です。
t検定
統計的仮説検定の一種であるt検定は、標本同士の平均値の差が有意か否かを検定するものです。
帰無仮説と対立仮説は以下のようになります。
対立仮説=平均に有意差がある
標本同士の平均値の差を見積もるときに「t値=(標本平均の差)/(標本平均の差の標準誤差)」を求めます。
この「t値」は、「自由度」と「t分布」に従うことがわかっています。
t分布の場合の自由度とは、平均値が固定された場合に自由にとりうるデータの数のこと。
詳細な説明は省きますが、このt値からP値を求めることができるので、0.05>P値が確認できれば帰無仮説が棄却され、対立仮説が採択されることになります。
t検定では「自由度」が大きな意味を持ちます。
「自由度が大きい」というのは「サンプル数が多い」ということで、たくさんのサンプルで実験をすると帰無仮説が棄却されやすくなります。
F検定
統計的仮説検定の一種であるF検定は、標本同士の分散の差が有意か否かを検定するものです。
対立仮説=分散に有意差がある
F検定は分散分析でよく用いられますので、詳細はそちらで。
カイ2乗検定
カイ2乗検定は、帰無仮説が正しければ検定統計量が漸近的にカイ二乗分布に従うような統計的検定法の総称です。
カイ2乗検定では、母集団についての特定の分布を仮定する必要がなく、このような検定法をノンパラメトリック検定と言います。
パラメトリック検定とは、母集団の分布がある特定の分布(正規分布など)に従うことがわかっている場合に用いる検定です。
カイ2乗検定によって算出されたカイ2乗値(χ2値)をもとにカイ2乗分布を確認します。
算出されたカイ2乗値を、総度数×(行列と列数の小さい方の数-1)で割り、全体の平方根を取ったものが「クラメールの連関係数」となります。
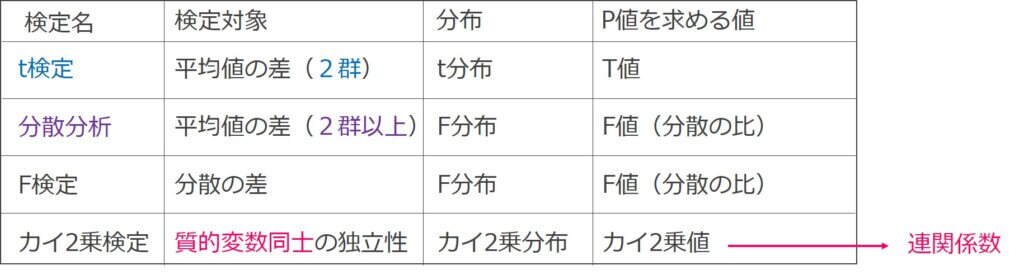
過去問
第1回 問113
心理学研究で行われている統計的仮説検定において利用される有意水準の説明として、最も適切なものを1つ選べ。
① 帰無仮説が真であるとき帰無仮説を棄却する確率である。
② 帰無仮説が真であるとき帰無仮説を採択する確率である。
③ 対立仮説が真であるとき帰無仮説を棄却する確率である。
④ 対立仮説が真であるとき帰無仮説を採択する確率である。
選択肢①が正解です。有意水準とは、可能性は小さいながらも帰無仮説が正しい可能性があり、その場合に誤って棄却してしまう確率です。
有意水準が危険率と呼ばれていることを覚えておけば、帰無仮説が真なのに誤って棄却してしまう確率のことという解釈ができます。
第3回 問7
統計的仮説検定の説明として、正しいものを1つ選べ。
① t検定では、自由度が大きいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい。
② 2つの条件の平均に有意な差が認められない場合、それらの平均には差がないといえる。
③ K.Pearson の相関係数が0.1%水準で有意であった場合、2つの変数間に強い相関があるといえる。
④ 対応のない2群のt検定では、各群の標準偏差が大きいほど、有意な差があるという結果が生じやすい。
⑤ K.Pearson の相関係数の有意性検定では、サンプルサイズが小さいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい。
① t検定では、自由度が大きいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい。
正しいです。自由度が大きい=サンプル数が多いほど、帰無仮説が棄却されやすくなります。つまり帰無仮説の棄却限界値が小さくなります。
② 2つの条件の平均に有意な差が認められない場合、それらの平均には差がないといえる。
間違いです。平均の有意差はt検定ですが、「有意な差が認められない」というのは、「帰無仮説が棄却できなかった」ということですが、「帰無仮説が棄却されない」=「帰無仮説が正しい」とは言えません。
③ K.Pearson の相関係数が0.1%水準で有意であった場合、2つの変数間に強い相関があるといえる。
間違いです。ピアソンの相関係数は「0」なら相関なし、「1」や「-1」なら相関が強いというように、相関係数の値自体で相関の強さが分かります。
相関係数が有意であった場合に断定できるのは「相関係数が0ではない」ということだけです。
④ 対応のない2群のt検定では、各群の標準偏差が大きいほど、有意な差があるという結果が生じやすい。
間違いです。「対応のない」というのは対象が異なるということです。
「t値=(標本平均の差)/(標本平均の差の標準誤差)」なので標準偏差が大きいほどt値は小さくなるので有意差があるという結果が生じにくいことになります。
⑤ K. Pearson の相関係数の有意性検定では、サンプルサイズが小さいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい。
間違いです。選択肢①と関連しますが、サンプルサイズが小さい=自由度が小さいほど、帰無仮説は棄却されにくくなりますので、帰無仮説の棄却限界値は大きいです。

この問題は、実際にt分布表を用いてt検定をやったことのある人でないと解けませんねぇ。
次の記事
次は、いよいよ具体的な分析手法に入っていきます。
まずは、分散分析について。




コメント