1変数や2変数の場合、ヒストグラムやクロス集計表で分析できます。
変数が多くなった場合に、どのように分析すればよいのでしょうか。
その手法が多変量解析です。
ここでは、試験の結果を多変量解析で分析してみましょう。
多変量解析として、因子分析、主成分分析、クラスター分析、重回帰分析、判別分析、ロジスティック回帰分析を見ていきます。
各分析方法がどのような意味を持っているのか、まずはイメージだけつかんでください。
それぞれの分析の詳細は別記事で。
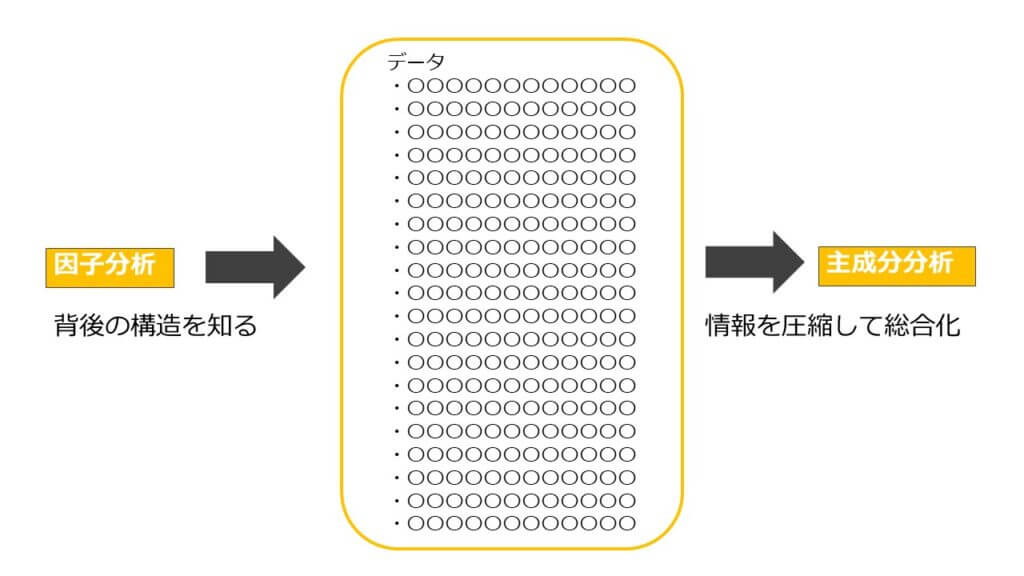
「要約」するための分析手法
様々な多変量解析は、その目的別に2種類に分類できます。
「要約」と「予測」です。
因子分析
因子分析は、データの裏に隠れている因子を見つける分析方法です。
例えば、試験の点数に影響している因子には何が想定できるでしょうか。
考えてみると、「勉強時間」「知能指数」「家庭環境」などの因子があると想像できます。
つまり勉強時間が長いほど点数は高い、知能指数が高いほど点数は高い、家庭環境が良好なほど点数は高い、など全てが点数に関係していることが想像されます。
別の例では、パーソナリティ理論があります。
パーソナリティ理論は類型論と特性論に分けられましたが、特性論では人の性格を決める様々な因子が提唱されていました。

キャッテルは16因子、ビッグファイブなら5因子がありましたね。
これも因子分析によって見出されたものです。
つまり、人にはいろいろな性格がありますが、その根底にある因子を見出したわけです。
このように、因子分析はデータの元になっている因子を見つけるものです。
詳しくは以下の記事で。

主成分分析
主成分分析は、たくさんの変数を少ない変数に置き換えて要約することで、データを理解しやすくする分析手法です。
以下の試験の点数を主成分分析により要約したい場合、Aさん、Bさん、Cさんの点数を単純に合計して要約すると、例えば02年度の点数は皆さん高いので易しかったと思われますが、この年度の1点の重みは他の年度と比べて軽いです。
| 受験者 | 00年度 | 01年度 | 02年度 |
|---|---|---|---|
| Aさん | 80点 | 85点 | 112点 |
| Bさん | 70点 | 79点 | 109点 |
| Cさん | 75点 | 76点 | 101点 |
つまり単純な合計点数ではAさん、Bさん、Cさんの比較はできないので、1点の重みを勘案して合計点数を出します。
このような要約をすると、情報量はある程度削減されつつも、ある程度の情報量は保てるので、良い要約ができたことになります。
これが主成分分析です。
先ほどの因子分析も主成分分析も、どちらもデータを要約する手法ですが、因子分析はデータの元となる因子を導くのに対して、主成分分析はデータを重み付けして要約・整理するという点で根本的に異なります。

ただし、扱うデータによっては同じ結果が得られる場合もあるので、実際にやってみると違いが分からなくなることも・・・
クラスター分析
クラスター分析は、様々なものが混ざり合っている集団の中から、互いに似たものを集めてクラスターを作り分類する方法です。
試験の点数の高い優秀組というクラスターを作ったり、合格した人というクラスターを作ったり。
以下の表では、例えばAさん~Eさんは点数が高いクラスター、Fさん~Jさんは点数が低いクラスターと分類できます。
| 受験者 | 19年度 | 20年度 | 21年度 |
|---|---|---|---|
| Aさん | 80点 | 85点 | 112点 |
| Bさん | 70点 | 79点 | 109点 |
| Cさん | 75点 | 76点 | 101点 |
| Dさん | 85点 | 87点 | 125点 |
| Eさん | 81点 | 83点 | 115点 |
| Fさん | 46点 | 52点 | 80点 |
| Gさん | 50点 | 55点 | 80点 |
| Hさん | 57点 | 60点 | 70点 |
| Iさん | 51点 | 66点 | 78点 |
| Jさん | 49点 | 69点 | 78点 |
これまで見てきた因子分析、主成分分析、クラスター分析は、データを「要約」して整理することが目的です。
データを要約することで直観的に分かりやすくするのです。
「予測」するための分析手法
ここからは、データを要約するのではなく、データを予測することが目的の分析です。
重回帰分析
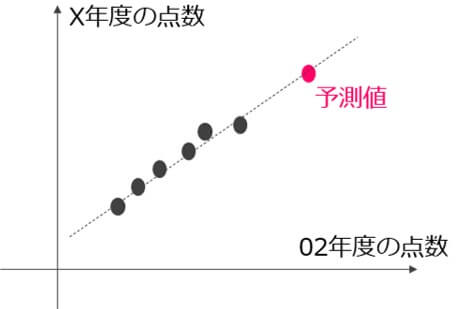
重回帰分析は、例えば以下の表にあるように、00年度~02年度の点数を元にして、X年度の点数を予測する等の分析です。
「X年の点数=a(00年の点数)+b(01年の点数)+c(02年の平均点)+ d(X年の平均点)」のような感じに。
| 受験者 | 00年度 | 01年度 | 02年度 | X年度 |
|---|---|---|---|---|
| Aさん | 80点 | 85点 | 112点 | ?点 |
| Bさん | 70点 | 79点 | 109点 | ?点 |
| Cさん | 75点 | 76点 | 101点 | ?点 |
上記の例では3変数ありますが、1変数の場合は「単回帰分析」といいます。
例えば以下のように02年度の点数とX年度の点数に直線的な相関が見られれば、直線を想定して02年度の点数がわかればX年度の点数も想定できます。
判別分析
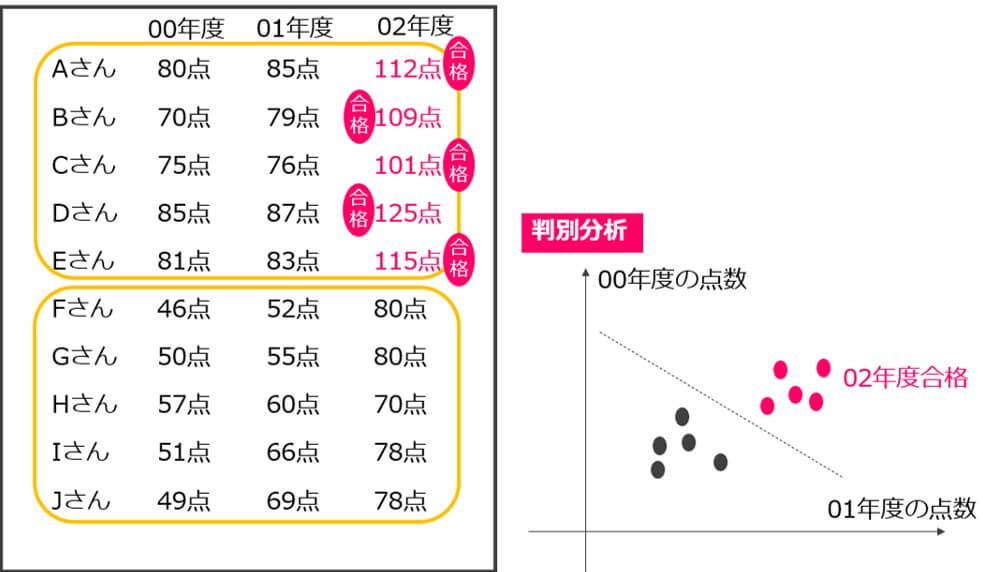
判別分析は、事前に与えられているデータが2つのグループに分かれている場合、新しいデータが得られた際に、どちらのグループに入るのかを判別するための分析手法です。
例えば、下の図にあるように00年度と01年度の点数を見れば、02年度の合否が予測できます。
このような場合に判別分析で合否を判別します。
ロジスティック回帰分析
ロジスティック回帰分析は、判別分析のように2つのグループの判別を目的とし、説明変数の効果を分析します。
判別分析では、2グループのどちらに入るかだけを判別しましたが、ロジスティック回帰分析では、未知データが一方のグループに入る確率を見出します。
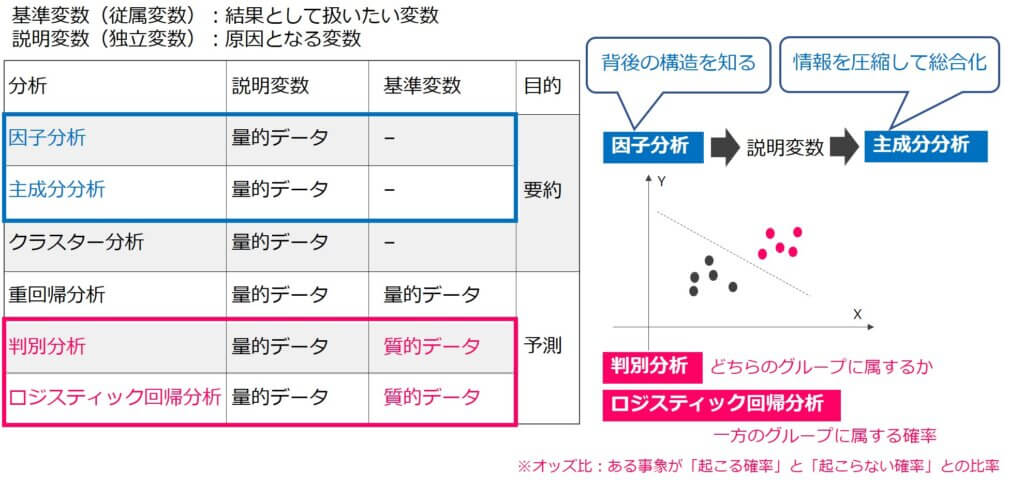
基準変数&説明変数
説明変数(独立変数):原因となる変数

これまで見て来たテストの点数という元データが「説明変数」だね。
主成分分析では、説明変数を基にして基準変数を求めますが、因子分析では、基準変数を基にして説明変数を求めていきます。 つまり主成分分析と因子分析は、データを説明できる要素を新たに作り出すという点においては類似していますが、実際のプロセスや考え方は真逆の分析です。
| 分析 | 説明変数 | 基準変数 | 目的 |
|---|---|---|---|
| 因子分析 | 量的データ | – | 要約 |
| 主成分分析 | 量的データ | – | |
| クラスター分析 | 量的データ | – | |
| 重回帰分析 | 量的データ | 量的データ | 予測 |
| 判別分析 | 量的データ | 質的データ | |
| ロジスティック回帰分析 | 量的データ | 質的データ |
上の表にあるように、多変量解析は量的データから量的データを導くものが多いですが、基準変数として質的データを扱う「判別分析」と「ロジスティック回帰分析」は、特徴的に覚えておきましょう。
まとめ
様々な多変量解析を見てきましたが、目的は2種類に分けられます。
説明変数から「予測」して基準変数を求めるのが、重回帰分析、判別分析、ロジスティック回帰分析です。
説明変数を「要約」して整理するのが、主成分分析、因子分析、クラスター分析です。
| 多変量解析の目的 | |
|---|---|
| 予測 | 要約 |
|
重回帰分析(量→量) |
主成分分析 因子分析 クラスター分析 |
それでは、すべての分析手法を下の表をもとに、おさらいしましょう(ここからの内容は下の動画で解説します)。
まずは、Aさん~Jさんの社会福祉士国家試験の点数が、00年度~02年度まであるとします。
この10名は00年度、01年度と不合格で02年度を受験したとします。
まず、因子分析は、これらの点数の裏に隠れている因子を探す分析でした。
たとえば、勉強時間や家庭環境、経済的余裕度、流動性知能、結晶性知能などの因子が、試験の点数を決めているというように、各因子が見出せます。
次に主成分分析は、試験の点数を要約するために合計点数を算出しますが、年度ごとに試験の難易度が異なり平均点も異なるので、その重み付けをして合計点数を算出します。
そうすれば、もともとの情報量をある程度保ったまま、情報を要約できたことになります。
-1-1024x576.jpg)
クラスター分析は、Aさん~Eさんの点数の高い組と、Fさん~Jさんの点数の低い組に分ける等、クラスターに分類する分析です。
ここまで見て来た因子分析、主成分分析、クラスター分析は、説明変数(量的データ)を要約することが目的です。
次は、「予測」が目的の重回帰分析、判別分析、ロジスティック回帰分析です。
重回帰分析は、00年度~02年度の点数を元にして、X年度の点数を予測する等の分析です。
「X年の点数=a(00年の点数)+b(01年の点数)+c(02年の点数)」のような感じに。
判別分析では、上の表のように00年度と01年度の点数から、02年度の合否を判別します。
講義動画
過去問
第2回 問7
量的な説明変数によって1つの質的な基準変数を予測するための解析方法として、最も適切なものを1つ選べ。
① 因子分析
② 判別分析
③ 分散分析
④ 重回帰分析
⑤ クラスター分析
説明変数は元になるデータのこと、基準変数は求めたい結果のこと。
説明変数である量的データから基準変数である質的データ導くのは、②「判別分析」でした。
例えばテストの点数という量的データから、合否という質的データの判別をするんでしたね。
第3回 問81
個体を最もよく識別できるように、観測変数の重みつき合計得点を求める方法として、最も適切なものを1つ選べ。
① 因子分析
② 重回帰分析
③ 主成分分析
④ 正準相関分析
⑤ クラスター分析
これは、③「主成分分析」が正解です。
観測変数を要約する分析として因子分析と主成分分析とクラスター分析がありますが、観測変数を重み付き合計点数などでまとめて総合化して要約する手法が主成分分析です。
精神保健福祉士 第22回 問題18
成人の勤労者を対象に、職場でのストレスの大きさ、職場でのサポートの程度及び抑うつ症状の重症度について、一定の尺度を用いた質問紙調査を行った。調査で得られた量的データを基に抑うつ症状を従属変数として、職場でのストレス及び職場でのサポートの二つの独立変数との関連性について分析を行った。次のうち、上記のデータ分析方法の名称として、正しいものを1つ選びなさい。
1 カイ2乗検定
2 デルファイ法
3 重回帰分析
4 分散分析
5 因子分析
事例より、「抑うつ症状=A×ストレス+B×サポート」という関係性を想定し、抑うつ症状がストレスとサポートから予測できるようにするということなので、選択肢3「重回帰分析」が適切です。
因みに「カイ2乗検定」は、2つの変数に対する2つの事象が互いに独立しているか、または観測された値と期待される理論的な値が適合するかを検定するものです。
「デルファイ法」は質的調査の一種で、専門家グループなどが持つ直観的意見や経験的判断を反復的に調査し、意見を集約・収束させていく手法です。
次の記事
次で、心理統計学(データ分析)が終了します。
最後は研究倫理について。




コメント
とても丁寧にわかりやすい説明をありがとうございます!
まだまだ理解不足の部分が多いので、何度も読み返し知識を深めていきます。
今後もどうぞよろしくお願いします!
心理統計学はここからどんどん記事を追加していきます。まずは因子分析から、頑張って〰️!