因子分析は、多変量データの裏側に潜む共通因子を探り出すための手法です。
心理検査(性格検査)では、たくさんの質問項目から、因子分析によってその裏に隠れているパーソナリティ(性格)を見出します。

キャッテルの16因子、ビッグファイブの5因子、ギルフォードの13因子などなど、覚えていますか?
ここでは、ギルフォードの13因子から12因子を抽出して性格検査に用いた「YG性格検査(矢田部ギルフォード性格検査)」を取り上げて、因子分析とはなんたるかを見ていきましょう。
心理検査、パーソナリティ理論、心理統計学が同時に勉強できる一石三鳥の内容です。
相関行列
YG性格検査は、人の性格に関する120問の質問に対して、「はい」「いいえ」「どちらでもない」の3つの選択肢のうちのどれかを選んで答え、パーソナリティの12特性を測定するものです。
「どちらでもない」:1点
「いいえ」:0点

これは順序尺度に見せかけて、等間隔なので間隔尺度だね。
因子分析の対象は間隔尺度か比例尺度なので、間隔尺度にすることで因子分析ができます。
①小さなことでもなかなか決断できない。
②淋しいのでだれかにそばにいてほしいと思うが、気軽に人に会う気はしない。
③お洒落どころか身だしなみにも興味がもてない。
④すぐに涙ぐむ。
⑤いったん怒り出すと自分がおさえられない。
・・・
ある人が検査した結果を示します。

たくさんの結果が集まると、例えば質問①が高得点の人は質問②も高得点だとか、質問同士の相関が見えてきます。
それらをもとに、それぞれの質問の相関係数を求めて下のような相関行列を導き出します。

因子分析は、相関行列を求めるところからはじまるよ。
例えば、質問①と質問②にはほとんど相関がないので0.1、質問②と質問③にはある程度の相関があるので0.5などとなっています。
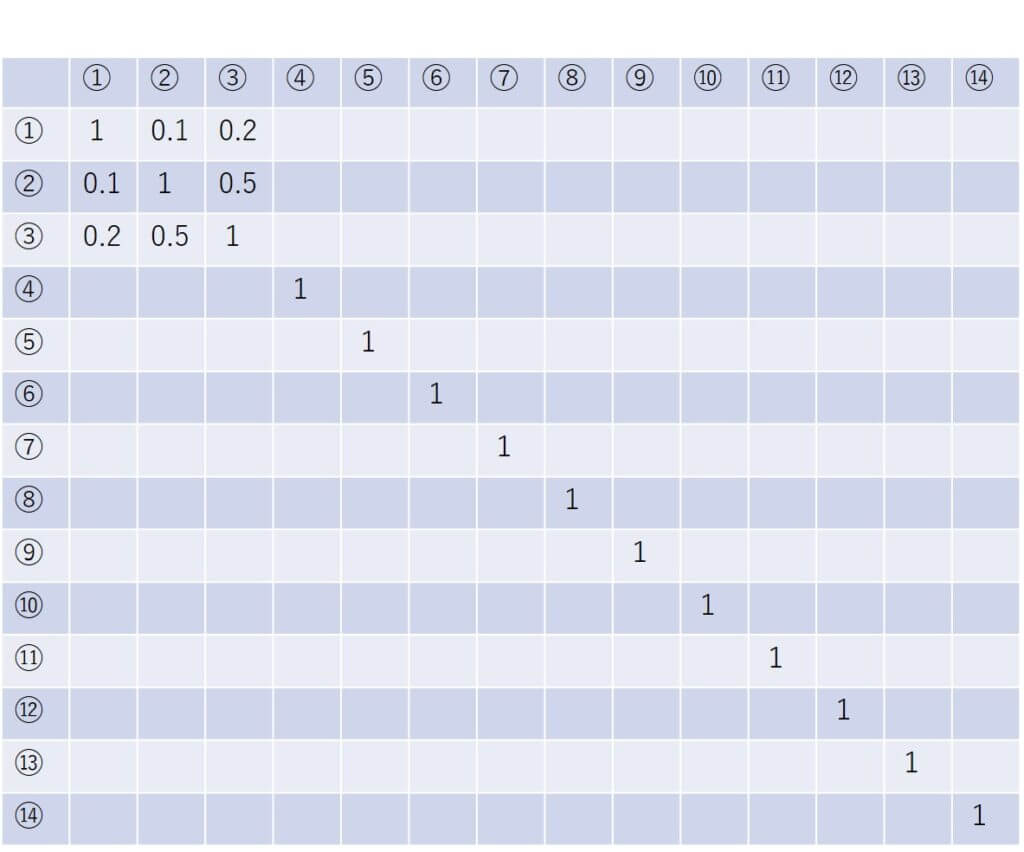
このような質問同士の相関から、その背後に隠れている共通因子を導くのが因子分析です。

例えば、質問①と質問④と質問⑦は大きな相関があるなぁ、そしたらその背後にはなにか共通する因子があるんじゃないのかなぁ、って感じだね。
この分析には、最尤法(さいゆうほう)、主因子法、最小二乗法など様々な手法があり、「因子負荷」を求めていきます。
ここからは因子分析のキモとなる「因子負荷」とは何か、見ていきましょう。
因子負荷
YG性格検査の120の質問で評価できるのは以下の12因子です。
この12因子を導き出すために、因子分析を用いて苦労して見出したのです。
その方法を見ていきましょう。
・協調性
・活動性
・神経質
・社会性
・劣等感
・思考性
・支配性
・抑うつ性
・気分変化
・客観性
・攻撃性
・のんきさ
先ほどの120の質問の裏には、これら12の因子が隠れているというわけです。
そして120の質問それぞれに12の因子が複雑に影響を与えています。
例えば下図において、「活動性」という因子は質問②に大きく影響し、質問⑩にはわずかに影響し、質問①などには全く影響しないということを表しています。
さらに各質問には、その質問にしか影響しない独自因子も想定します。
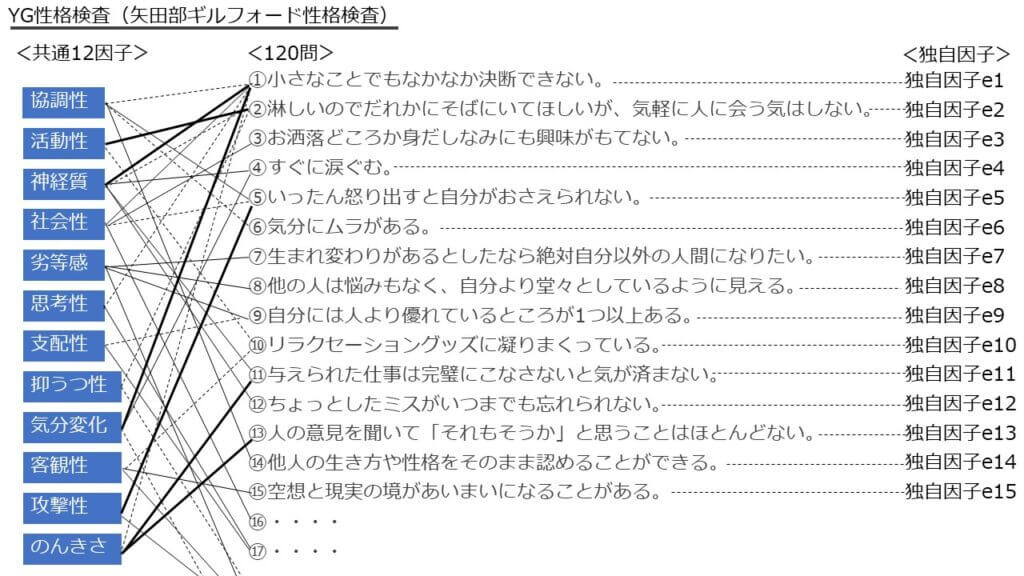
上記を方程式に表すと、
②=0.0×協調性+1.0×活動性+0.1×神経質+0.0×社会性+0.0×劣等感+・・・+独自因子e2
③=0.2×協調性+1.0×活動性+0.5×神経質+1.0×社会性+0.1×劣等感+・・・+独自因子e3
④=0.0×協調性+0.3×活動性+1.0×神経質+0.0×社会性+0.1×劣等感+・・・+独自因子e4
⑤=0.8×協調性+0.1×活動性+1.0×神経質+0.5×社会性+0.0×劣等感+・・・+独自因子e5
・・・
因子負荷量が0.0では全く相関がない、つまりその質問にその因子は関係しないことを表します。
この「因子負荷量」が、先ほどの相関行列から最尤法などを用いて導くものです。
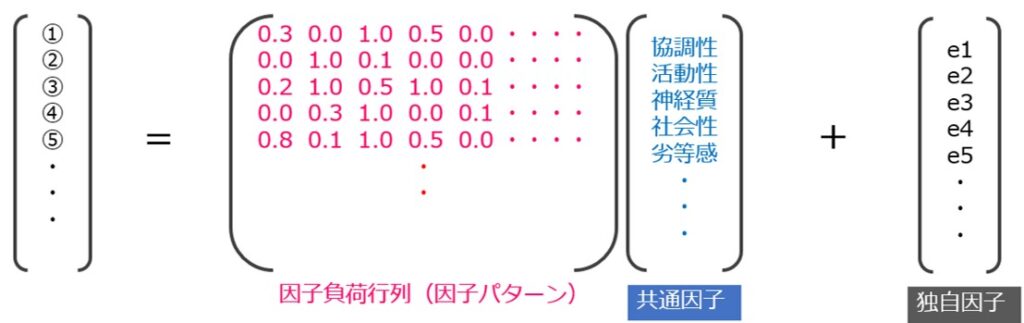
このように、各質問(観測変数)は、様々な質問に影響を与える「共通因子」と、その質問だけに影響する独自因子に分けられ、因子分析で求めるのは「共通因子」のほうです。
そして共通因子の重みとなる係数のことを「因子負荷量」と呼んでいます。
この因子負荷量を行列にしたものを「因子負荷行列(因子パターン行列)」と呼んでいます。
ここで以下の2つの用語の意味を押さえておきましょう。
独自性:1-共通性
直行回転と斜行回転
ここまで、各因子とその重みである因子負荷量を求めてきました。
しかしこのように求めた因子や因子負荷量は、完全に感覚的なものです。
そもそも因子の名称は自分で決めなければなりません。

つまり、質問①と質問②に共通する因子だから、この因子を「協調性」と名付けようなどと決めるわけだね。
さまざまな質問項目に共通する因子は、無限に想定できます。
つまり因子の名称がうまく命名できるようなわかりやすい「因子負荷量」となるような因子を見出していくのが因子分析ということです。
最初に最尤法などで見出した因子負荷量は初期値にすぎません。
解釈しやすい因子負荷行列(因子パターン行列)が出てくるまで、因子軸を回転させて、試行錯誤していくのです。
例えば下図の左のような因子1と因子2を見出しても、命名するのに苦労します。
なぜなら因子負荷量の多くが値を持ってしまうので、その因子がどのような意味を持つのか分かりにくいからです。
そこで右にあるように軸を回転させてやって、限定された観測変数に影響を与える因子Aや因子Bのような軸を見出すのです。
そうすることで因子の解釈が容易になり命名しやすくなります。
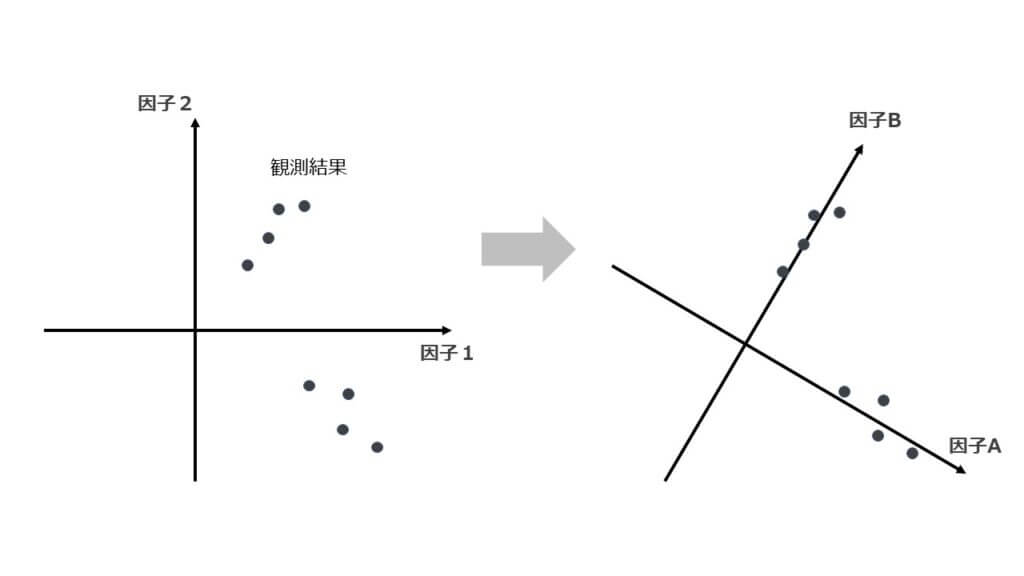
さらに上図は因子軸が直行しているように書きましたが、直行している必要もありません。
因子軸同士が直行するということは、その因子同士に相関がないことを意味します。
直行しているベクトルはそれぞれの成分を持ちえませんから。

例えばパーソナリティ理論で導かれた因子は、ビッグファイブなら「外向性」「調和性」「誠実性」「神経症的傾向」「経験への開放性」の5因子。これらはそれぞれに相関の無い直行ベクトルのイメージがありますね。しかし因子同士に相関がある斜行ベクトルでも構わないわけです。
ではどのような基準で回転させればよいのでしょう。
直行回転:バリマックス回転
直行回転の代表例は、バリマックス回転(varimax rotation)です。
これは「因子負荷量の二乗を因子内分散の和を最大にするように直行行列を用いて回転」する手法です。
バリマックスの「バリ」は「分散(バリアンス)」のこと、つまり分散をマックス(最大)にする回転方法が、バリマックス回転です。
斜行回転:プロマックス回転
直行回転は軸が直角という制約のもとで回転させますが、斜行回転はその制約がないので、因子を解釈しやすい結果を与えることが多いので、よく用いられます。
プロマックス回転(promax rotation)は、「バリマックス回転+プロクラステス回転」の合成語です。
プロクラステス回転とは、ターゲットとなる因子負荷行列に最小二乗基準で最も近くなるように回転する方法で、例えば、先に得られた因子負荷行列に近い解を得たい場合などに使えます。つまり、プロマックス回転では、バリマックス回転の解に近い斜交回転が可能になります。
因子構造
ここでは「因子構造」の意味と、因子負荷と因子構造の違いを図を見ながら理解していきましょう。
因子構造とは、各観測結果と各因子との相関係数を要素とする行列です。
下図にあるように、観測結果は共通因子と独自因子に分けられるのでした。
この共通因子を様々な回転によって見出していくのが因子分析です。
下の図にあるように因子1と因子2を想定して、共通因子を青と緑のベクトルに分解すると、そのベクトルの絶対値が「因子負荷量」になります。
対して、因子構造とは、共通因子から因子軸それぞれに降ろした垂線との交点の値になります。
つまり、因子構造は観測結果と因子との相関係数ですから、観測結果がどの程度その因子に関係しているかを表すものです。
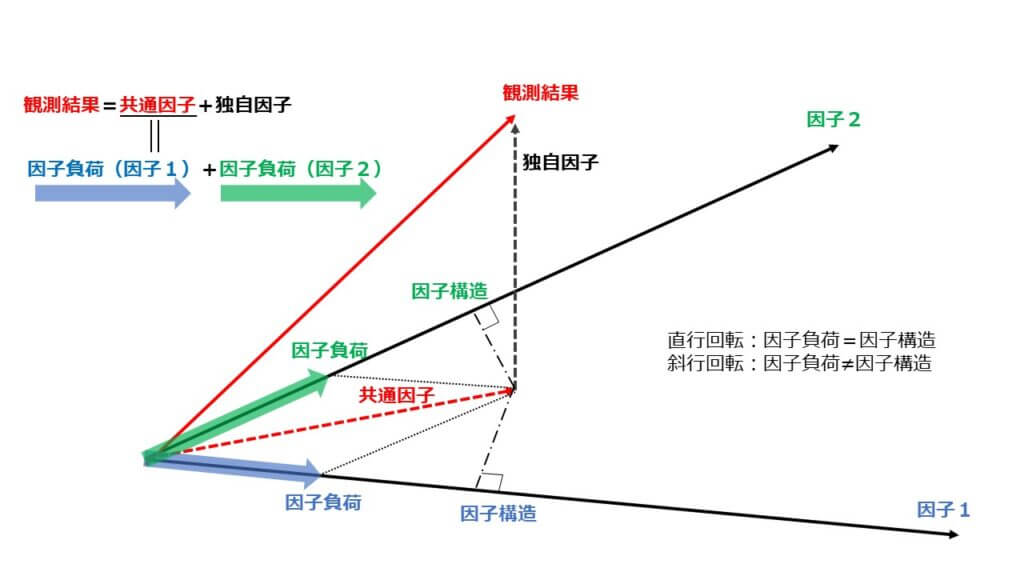
上の図では、因子1と因子2が斜行していますが、直行していれば、因子負荷と因子構造は同じ値になることがわかりますね。
まとめ
とても難しい内容でしたが、ここまでの因子分析の流れをまとめます。
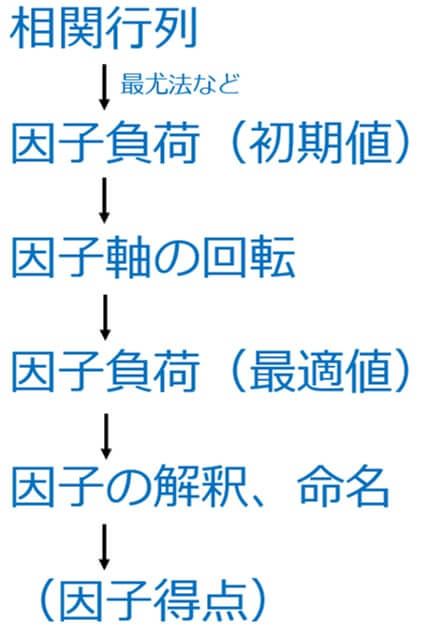
まずは観測結果同士の相関を表す相関行列を求めます。
そこから最尤法などを用いて「因子負荷行列」を求めます。
この初期解を回転させながら、解釈しやすい因子を見出していきます。
因子が解釈できるようになれば、その因子に名前をつけます。
これが因子分析です。
最後に「因子得点」を求めることもあります。
因子得点とは、それぞれのデータに対する共通因子の値のことです。
過去問
第1回 問8
パーソナリティや自我状態に関する心理検査について、正しいものを1つ選べ。
① MAS は、多面的にパーソナリティを測定する検査である。
② IAT は、顕在的意識レベルの自尊心の個人差を測定する検査である。
③ NEO−PI−R は、パーソナリティの6つの次元を測定する検査である。
④ 東大式エゴグラムは、被検者の自我状態をP、A又はCの3タイプのいずれか1つに分類する検査である。
⑤ YG性格検査は、パーソナリティの12の特性を測定する120項目への反応を通して被検者を典型的な型に分類する検査である。
選択肢⑤が正解です。今回の記事で⑤は忘れませんね。
その他の選択肢は「心理検査」で詳しくやります。
第5回 問80
G.W.Allport や R.B.Cattell らの特性論の考えを引き継ぎ、L.R.Goldberg が指摘した性格特性理論の基盤となっている統計手法として、適切なものを1つ選べ。
① 因子分析
② 分散分析
③ 共分散分析
④ 重回帰分析
⑤ クラスター分析
選択肢①が正解です。
第1回 問6
因子分析の斜交回転において各観測変数と各因子との相関係数を要素とする行列を表すものとして、正しいものを1つ選べ。
① 共通性
② 独自性
③ 因子構造
④ 因子負荷
⑤ 単純構造
斜行回転なので、選択肢③「因子構造」が正解です。
もし、直行回転なら「③因子構造」と「④因子負荷」が同じ値になりますので選択肢④も正解になります。
第4回 問6
因子分析による解析を計画している調査用紙の回答形式として、最も適切なものを1つ選べ。
① 順位法
② 一対比較法
③ 自由回答法
④ 評定尺度法
⑤ 文章完成法
① 順位法
順位法は順位を答えさせるもので、順序尺度が得られます。
因子分析では順序尺度ではなく間隔尺度や比例尺度が対象となりますので、不適切です。
② 一対比較法
一対比較法は、例えば「AとBを比較してどちらかを選択」「BとCを比較してどちらかを選択」というよう一対を比較する方法で、最終的にAとBとCの順位をつけます。これも順位法と同じように基本的には順序尺度になるので因子分析には不適切です。
③ 自由回答法
自由回答法は、自由に回答するので得られるのは質的データです。なので因子分析はできません。
④ 評定尺度法
評定尺度法は、例えば「①非常に当てはまる、②ある程度当てはまる、③どちらでもない、④あまり当てはまらない、⑤全く当てはまらない」などのようなリッカート尺度による質問に解答する手法です。これは基本的には順序尺度なんですが程度表現を適切に用いれば間隔尺度として扱えますので、因子分析に用いることができます。ということでこれが正解です。
⑤ 文章完成法
文章完成法は、未完成の文章を完成させる心理検査です。因子分析の対象ではありません。
次の記事
次は、重回帰分析について。




コメント