【心理統計学】独立変数＆従属変数、代表値＆散布度、４尺度＆リッカート尺度、天井効果＆フロア効果

心理統計学

2022.06.032022.04.18

心理師や心理カウンセラーになるためには、研究者や科学者としての能力も求められます。

まずは、心理統計学の基礎から見ていきましょう。

独立変数＆従属変数
剰余変数
代表値＆散布度
４尺度
まとめ
天井効果＆フロア効果
過去問
次の記事

独立変数＆従属変数

統計学の実験は、実験者が操作する変数（独立変数）と観測される変数（従属変数）によって組み立てられます。

独立変数というインプットによって従属変数がアウトプットされるということですね。

しかし従属変数に影響を与えるのは実験者が操作する独立変数だけではなく、実験者が操作しない様々な要因があります。

このような様々な要因を「剰余変数」と呼びます。

独立変数は「説明変数」とも呼ばれます。

従属変数は「目的変数、基準変数」とも呼ばれます。

従属変数に影響するのは、独立変数と剰余変数ということです。

剰余変数

従属変数に影響を与えるのは、独立変数と剰余変数です。

独立変数の影響をしっかり見極めるために、剰余変数の影響はできる限り小さくしたいわけです。

そのために様々な方法があります。

一定化：剰余変数をできる限り一定に保つ
マッチング：影響力の大きい剰余変数をできる限り一致
バランス化：従属変数に影響を与えそうな変数について群間で同じ割合に割当て
カウンターバランス：参加者によって課題の順番を変えて残留効果を相殺
ランダム化（無作為化）：剰余変数の値を偶然に任せる

試行数が多いとカウンターバランスは無理なのでランダム化を用いることになりますね。

代表値＆散布度

統計データを要約するのは「代表値」と「散布度」の２つです。

「代表値」といえば、平均値、中央値、最頻値の３種類、「散布度」といえば、四分位偏差、不偏分散、標準偏差などです。

例えば、正規分布であれば、代表値として「平均値」、散布度として「分散（標準偏差）」が決まれば分布は決まりますね。

以下にある４種類の尺度によって、用いられる代表値と散布度がある程度決まっています。

４尺度

統計学に用いられる変数（尺度）には、４種類あります。

４種類の尺度の基礎的な内容は以下のページを参照してください。

【社会調査（量的調査）】統計学の４尺度、リッカート尺度とは？

名義尺度、順序尺度、間隔尺度、比例尺度の４つは理解が難しいですよね。それぞれの例を思い浮かべられるようになれば理解が深まります。リッカート尺度は４つのうちのどれでしょう。

尺度	特徴	例	代表値	散布度
名義尺度	分類	性別、血液型など	最頻値	平均情報量
順序尺度	順序、大小関係	ランキング、順位など	中央値	四分位偏差
間隔尺度	間隔	温度、知能指数など	平均値	不偏分散、標準偏差
比例尺度	ゼロ点の存在、比率の等価性	身長、体重	幾何平均値	変動係数（変異係数）

名義尺度の代表値は最頻値、順序尺度の代表値は中央値、間隔尺度や比例尺度の代表値は平均値、さらに比例尺度であれば幾何平均値も求めることができます。

ここまでは分かりやすいと思います。

分かりにくいのは散布度です。間隔尺度や比例尺度のような連続変数の散布度は「分散（標準偏差）」というのは分かりますが、では名義尺度や順序尺度の散布度はどうなるのか、これが分かりにくいと思います。

名義尺度の散布度は、「平均情報量」が用いられます。

平均情報量とは、総度数と各カテゴリー度数との比較、エントロピーともいいます。

順序尺度の散布度には、「四分位偏差」が用いられます。

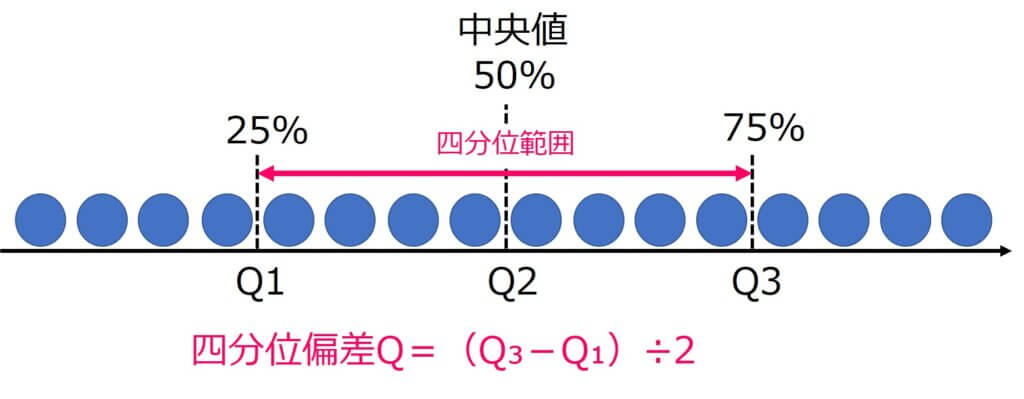
四分位偏差は、データを大きさの順に並べ全体を4分の1ずつ分け、下図のようにQ1、Q2、Q3を定めたとき、

四分位偏差Q＝（Q₃－Q₁）÷2

で求めることができます。

まとめ

４尺度で用いられる統計量をまとめます。

名義尺度では最頻値以外は意味がありませんが順序尺度になると中央値も意味を持ちます。

間隔尺度では平均値や分散、相関係数も計算でき、比例尺度になると、幾何平均値や調和平均値も意味をもちます。

幾何平均はn個の数の積のn乗根、調和平均は逆数の算術平均の逆数で定義されます。

一般的にイメージされる平均値は「算術平均」で、総和を足した数で割る平均値のことです。しかし比率や割合で変化する変数には「幾何平均（相乗平均）」、率の平均を求めるには「調和平均」を用います。

統計量	名義尺度	順序尺度	間隔尺度	比例尺度
最頻値	〇	〇	〇	〇
中央値	×	〇	〇	〇
平均値	×	×	〇	〇
分散	×	×	〇	〇
相関係数	×	×	〇	〇
幾何平均値	×	×	×	〇
調和平均値	×	×	×	〇

天井効果＆フロア効果

天井効果とは、測定値が最大値に偏ってしまい独立変数（説明変数）の効果が検出できないことです。

例えば、以下のような心理検査のリッカート尺度で、多くの回答が5点（最大値）の場合に天井効果、1点（最小値）の場合にフロア効果（床効果）が起こりやすいです。

＜リッカート尺度＞
１点：全く当てはまらない
２点：ほとんど当てはまらない
３点：どちらともいえない
４点：ある程度あてはまる
５点：完全に当てはまる

リッカート尺度は、順序尺度と間隔尺度の中間くらいのイメージで。

過去問

第2回問5

実験は実験者が操作する変数と観測される変数によって組み立てられるが、前者以外にも後者に影響を与える変数があることが多い。この変数は何か、正しいものを１つ選べ。
① 従属変数
② 剰余変数
③ 独立変数
④ 離散変数
⑤ ダミー変数

① 従属変数
間違いです。従属変数は観測される変数です。

② 剰余変数
これが正解です。

③ 独立変数
間違いです。独立変数は実験者が操作する変数です。

④ 離散変数
間違いです。離散変数は飛び飛びの値しかとらない変数です。
例えばサイコロの目とか。対して連続変数は連続する値を取る変数で、身長や体重は連続変数です。

⑤ ダミー変数
間違いです。ダミー変数は、本来数字でない変数を数字に置き換える変数です。
例えば「男性」→「1」、「女性」→「2」など。

第3回問8　

心理学の実験において、｢XがYに及ぼす影響｣の因果的検討を行うとき、正しいものを１つ選べ。
① Xを剰余変数という。
② Yを独立変数という。
③ 研究者があらかじめ操作するのは Y である。
④ Xは、値又はカテゴリーが２つ以上設定される。
⑤ 結果の分析には、XとY の相関を求めるのが一般的である。

① Xを剰余変数という。
間違いです。剰余変数ではなく独立変数（説明変数）です。

② Yを独立変数という。
間違いです。独立変数ではなく従属変数（目的変数、基準変数）です。

③ 研究者があらかじめ操作するのはYである。
間違いです。研究者があらかじめ操作するのはXです。

④ Xは、値又はカテゴリーが２つ以上設定される。
正しいです。一般的に独立変数が1つということはなく、複数あります。

⑤ 結果の分析には、XとYの相関を求めるのが一般的である。
間違いです。相関関係だけでは因果関係の証明にはなりません。

第4回問83

他者と比べて、自分についてよりポジティブな判断を行うかどうかを検討する目的で研究を行う。
他者に対する性格の評定と自分に対する性格の評定を同時に得る場合に、両者の評定を行う順序について適用するべき方法は何か、最も適切なものを１つ選べ。
① 一定化
② バランス化
③ マッチング
④ ランダム化
⑤ カウンターバランス

選択肢⑤が正解です。

第1回（追試）問119

心理学実験について、正しいものを１つ選べ。
① 行動に及ぼす要因を明らかにするために実験者が操作する変数を独立変数という。
② 剰余変数を統制するために、複数の実験者が入れ替わり実験を実施することが望ましい。
③ 実験者の期待や願望が意図せずして振る舞いに表れ、参加者に対して影響を及ぼすことをホーソン効果という。
④ 測定値が最大値に達することにより、説明変数の効果を検出する上で問題が生じることをキャリーオーバー効果という。

① 行動に及ぼす要因を明らかにするために実験者が操作する変数を独立変数という。
正しいです。

② 剰余変数を統制するために、複数の実験者が入れ替わり実験を実施することが望ましい。
間違いです。本来であれば剰余変数の影響は限りなく小さくしたいわけで、その目的のためには複数の実験者が入れ替わり立ち代わり実験をしていてはいけません。

③ 実験者の期待や願望が意図せずして振る舞いに表れ、参加者に対して影響を及ぼすことをホーソン効果という。
間違いです。これは「要求特性」の説明です。

④ 測定値が最大値に達することにより、説明変数の効果を検出する上で問題が生じることをキャリーオーバー効果という。
間違いです。これは「天井効果」の説明です。